The Level-1B algorithm enables generation of a Level-1B product from the precursor Level-1A product. The processing includes:
- radiometric corrections:
- inverse of on-board equalization
- equalization correction
- dark current correction including offset and non-uniformity correction (if equalization correction activated)
- blind pixels removal
- cross-talk correction including optical and electronic crosstalk correction
- relative response correction
- SWIR rearrangement
- defective pixels correction
- no data pixels correction
- restoration including deconvolution and denoising (optional). This correction is disabled by default in the Level-1B processing.
- binning for 60 m bands (B1, B9 and B10)
- radiometric offset addition to avoid truncation of negative values
- masks management including saturated Level-1B masks generation, no_data mask generation, defective masks generation.
- physical geometric model refinement
These steps are chained and activated for each band. Each algorithm step is described below; please refer to the Level 1 ATBD for more details about the algorithms.
Radiometric Corrections
The SENTINEL-2/MSI radiometric model is given by Equation 1:
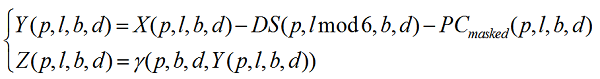
Equation 1: SENTINEL-2 Radiometric Model
Where:
- Y(p,l,b,d) is the raw signal of pixel p corrected from the dark signal and from the pixel contextual offset (expressed in Least Significant Bit (LSB))
- Z(p,l,b,d) is the equalized signal also corrected from non-linearity (expressed in LSB)
- ϒ(p,b,d,Y(p,l,b,d)) is a function that compensates the non-linearity of the global response of the pixel p and its relative behaviour with respect to other pixels
- DS(p,j,b,d), is the dark signal of the pixel p in channel b, for chronogram sub-cycle line number j (j is within 1 to 6)
- PCmasked(p,l,b,d) is the pixel contextual offset. It aims at compensating the dark signal variation due to voltages fluctuations with temperature.
Two different functions are required for modelling ϒ (p,b,d,Y(p,l,b,d)):
- a piece-wise linear (two parts: bilinear)
- a cubic (polynomial of degree 3)
For VNIR channels, the baseline is to consider a polynomial function of degree 3 to have a best fit of the detector response. For SWIR channel, the bilinear is the baseline option that will be used.
Inversion of the On-board Equalization
The bilinear equalization is applied on-board to both channels (VNIR and SWIR) and per detection line before compression to reduce compression effect on detector photo-response non-uniformity.
An inversion of the on-board equalization is performed to retrieve the original detectors response Xk(i,j) and further radiometric corrections are applied such as cross-talk correction and improved equalization processing.
As output a reverse equalized image (output image is called X in the mathematical description) is obtained.
Equalization Correction
The objective of equalization is to achieve a uniform image when the observed landscape is uniform. It is performed by correcting the image of the relative response of the detectors (if equalization correction is activated).
Dark Signal Correction
The dark signal correction involves correcting an unequalised image by subtracting the dark signal (if equalization correction is activated). The dark signal DS(i,j) can be decomposed as shown in Equation 2:
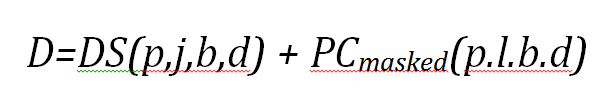
Equation 2: SENTINEL-2 Dark Signal
- a cyclic component that does not evolve with time: DS(p,j,b,d) is the dark signal of the pixel p in channel b, for chronogram sub-cycle line number j (j is within 1 to 6 for 10 m resolution band, 1 to 3 for 20 m band, and equal 1 for 60 m band);
- a residual with time: PCmasked(p,l,b,d) is the pixel contextual offset (Dark Signal Offset).
Dark Signal Non-Uniformity
Variability in the dark signal arises as a result of the different time required for integration by the individual bands. This signal varies as a function of the line number with a spatial frequency.
Defining a cycle by the integration time for 60 m bands, there are:
- six different working configurations, i.e. six different dark signals, for 10 m bands
- three different dark signals for 20 m bands
- one dark signal for 60 m bands.
For a given line 'i' in the image, the corresponding dark signal depends on the line number inside the area. The average of 'i' observations assumes that the same radiance is observed and allows noise reduction (Equation 3).
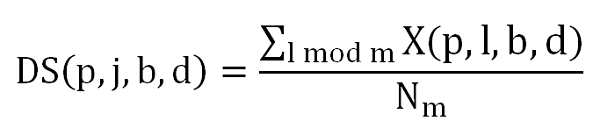
Equation 3: SENTINEL-2 Dark Signal Uniformity
where Nm is the number of lines being summed, and j is an index within the range [1,6] corresponding to the chronogram sub-cycle line numbe (j is within [1,6] range for 10 m bands, [1,3] for 20 m bands and [1,1] for 60 m bands).
DS(p,j,b,d) is determined as an average of the dark signal along the columns and therefore is independent of the line variable.
Dark Signal Offset
The offset variation of dark signal is due to voltage fluctuations. To compensate for this signal, an offset for each line is computed using blind pixels located at the extremity of each detector module. The number of blind pixels depends on the band (32 blind pixels for 10 m bands, and 16 blind pixels for 20 m and 60 m bands). For each band, each detector module and each line of the image, the offset is computed as the average value of the signal acquired by the valid blind pixels:

Equation 4: SENTINEL-2 Dark Offset Computation
where N is the number of valid blind pixels per detector module and l the blind pixel index and Inter_Image is the raw image corrected from the application of the Non-Uniformity Dark signal.
Blind Pixel Removal
For each band and each detector module, blind pixels are removed from the image product.
Crosstalk Correction
Crosstalk correction involves correcting parasitic signal at pixel level from two distinct sources: electronic and optical crosstalk (if equalization correction is activated).
In both cases, the parasitic signal of a pixel in a given band is modelled as a linear function of the signal in the other bands acquired at the same time and at the same position across track.
Relative Response Correction
Relative response correction involves correcting the image of the relative response of the detectors (if equalization correction is activated). The correction applies respectively a bilinear and a three-degree polynomial function to the SWIR and VNIR channels.
The coefficients of the polynomial function are made from sun diffuser observations during calibration mode; the BRDF of the diffuser being characterised before launch. An estimation of the coefficients for each instrument is performed at the same time as the estimation of the absolute radiometric calibration, i.e. every three repeat cycles (30 days). Assuming that the response of the instrument is a cubic function (e.g. VNIR channels) of the radiance, Eq. (1) can be written as:
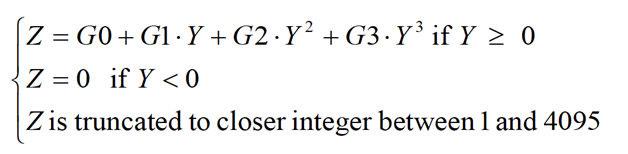
Equation 5: SENTINEL-2 Equalization Correction
In case of the SWIR band Equation (3) becomes:
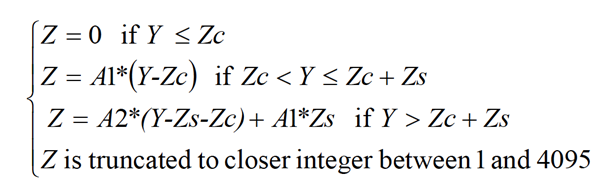
Equation 6: SENTINEL-2 Equalization Correction
where:
G3, G2, G1 and G0 are the parameters of the cubic model and A1, A2, Zc and Zs are the parameter of the bilinear model.
Equalization processing is performed for each non-defective pixel or non-blind pixel.
SWIR Rearrangement
Pixels of the SWIR bands (band 10, band 11 and band 12) are rearranged. For the SWIR bands, each detector module is composed of three lines for band 10 and four lines for band 11 and band 12. To make optimal use of the pixels with the best SNR for the acquisition, one pixel over three lines for band 10 and two successive pixels over four lines for band 11 and band 12 is selected for each column. In the instrument, these bands work in Time Delay Integration (TDI) mode and are re-arranged along columns on the ground. This algorithmic procedure ensures the best registration between columns of SWIR images.
For 20 m resolution bands (band 11, band 12), the shift to be applied is ± 1 pixel.
For 60 m resolution band (band 10), the shift to be applied is ± 1/3 pixel and is performed using a one-dimensional filter.
Defective Pixel Correction
Defective pixel correction involves allocating to a defective pixel, a value corresponding to the bicubic interpolated radiometry of its neighbouring pixels (if they are valid, and their value is greater than a threshold).
Defective pixels can arise as a result of:
- weak response that cannot be compensated for by equalization
- saturated response
- temporal instability
As well as the pixel position and the type of defect, the interpolation filter is provided in a GIPP. The maximum number of allowed adjacent defective pixels is defined by a threshold provided in a GIPP as well. If the number of adjacent pixels is outside the threshold, the correction is not applied.
Holes in the spectral filters can also affect the SENTINEL-2 images. The same correction as for defective pixels is applied.
Restoration
Restoration processing combines two actions:
- image de-convolution - applying a bi-dimensional spatial filter to the effect of the MTF to enhance the contrast
- image de-noising - performing a decomposition of the image in wavelet packets.
De-convolution processing compensates for blurring due to instrumental MTF. De-convolution is recommended when the MTF at Nyquist frequency is low, however, de-convolution processing increases the noise for high spatial frequencies, particularly over uniform areas. This phenomenon is limited by dedicated de-noising.
De-convolution is performed by Fourier Transform (FT) and the de-noising process is based on a thresholding technique of wavelets coefficients.
These restoration processes are currently disabled by default in the Level-1B processing. It is not recommended to use the restoration step because the instrument's MTF is already high enough.
Binning for 60 m Bands
For bands B1, B9 and B10, the spatial resolution is approximately 60 m along track and approximately 20 m across track. To achieve a homogeneous resolution (i.e. 60 m) both along and across track, these bands are filtered and sub-sampled in the across track direction. The filter and the sampling rate (3, by default) are provided in a GIPP by the IQP.
No Data Pixels
Pixels with no data generally correspond to missing lines within the image product. These pixels are identified in a mask provided with the product.
To correct for no data, and to insert a value, these pixels are interpolated using neighbouring valid lines. The interpolation filter is provided in a GIPP. A threshold for the maximum number of missing joined lines is defined. This threshold is provided in a GIPP. Beyond this threshold, no correction processing is applied.
Radiometric Offset
To avoid truncation of negative values, the dynamic range of both SENTINEL-2A and SENTINEL-2B is shifted by a band-dependent constant radiometric offset called RADIO_ADD_OFFSET and defined in a configuration file. The new pixel value is computed as following:
NewDN= CurrentDN - RADIO_ADD_OFFSET
Note that in the convention used, the offset is a negative value.
It is important to note that:
- the radiometric offset will have no impact on the generation of the numerical saturation value, as it will be added up after. Moreover, there will be no saturation due to this offset as the measured levels are far from the numerical saturation for Level-1B data. Indeed, for a 12-bit integer, numerical saturation is reached for a value of 4095.
- adding an offset for Level-1B would imply that this offset should be handled by the refining and should be subtracted before the Level-1C projection and TOA conversion.
Saturated Pixels
Saturated pixels are identified in a mask associated to the product. No correction is applied.
Geometric processing
After the radiometry step, and to improve the accuracy of geolocation performance, a geometric refinement can be carried out. This operation occurs before the orthorectification process for Level-1C products. It is performed on the full swath by the longest possible length in automatic mode.
Viewing model refining
The viewing model includes:
- a datation model for determining the exact start date of each line ,
- a tabulated orbital data, allowing to know the position of the spacecraft at the time of the line acquisition.
- a tabulated attitude data, allowing to know the orientation of the spacecraft at the time of the line acquisition.
- the viewing directions in the spacecraft piloting frame.
The viewing model allows to compute the viewing vector (line of sight) at the time of the pixel acquisition. By intersecting this viewing vector with an Earth model, it is possible to compute the geolocation (or direct location) of the pixel, and inversely, to determine the position of a point on the ground in the image (Image location or inverse location).
However, the attitude and orbital data are known with a given precision, due to the sensors inaccuracy: GPS, attitude sensors. Additionally, thermo-elastic effects at the scale of the orbit can also impact the accuracy of the geolocation. To improve the geolocation performance, geometric refining can be applied by adding polynomial corrections to the viewing model.
To correct the position data, a polynomial function of time is estimated. The polynomial coefficients are estimated by a mean square regression called the spatio-triangulation. The polynomial functions coefficients, correcting the attitude and orbital information used by the location functions (geolocation function and inverse location function), are computed so as to minimise the average residual values (cf. Figure 1) of a large number of Ground Control Points (GCP). To sum up, the refining outputs are the polynomial functions correcting attitude and orbital data.
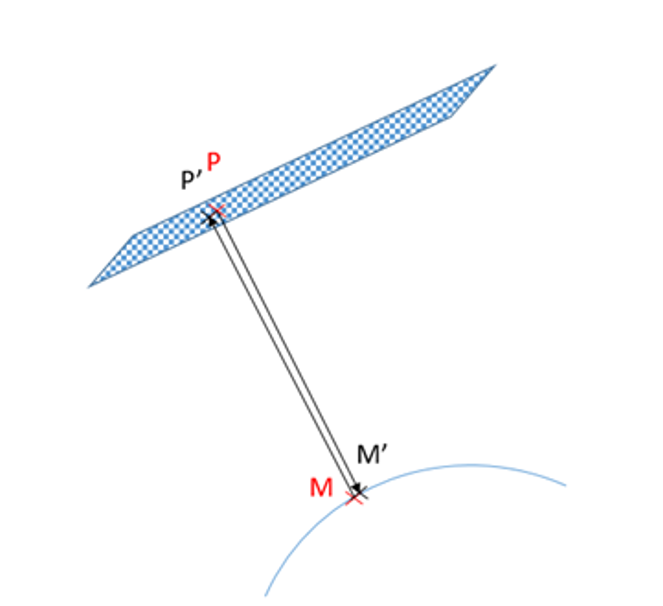
Figure 1: Illustration of residuals distance values (P-P') and (M-M')
Ground Control Points Selection
Common geometry resampling
To find the GCP necessary to the refining, a correlation is performed between the reference segment and the segment to refine. This correlation is high when images with similar spectral contents, at a similar resolution and in a similar geometry are used.
The first two conditions are guaranteed by using one reference spectral band for the correlation process. The reference cover is called the Global Reference Image (GRI).
The GRI is a set of globally acquired, cloud-free, mono-spectral (B4, red channel) Level-1B Sentinel-2 images. The GRI, illustrated in Figure 2, is composed of roughly 1000 images. The cloudy areas are constituted of a stack of overlapping images in order to limit clouds and ensure a full coverage.
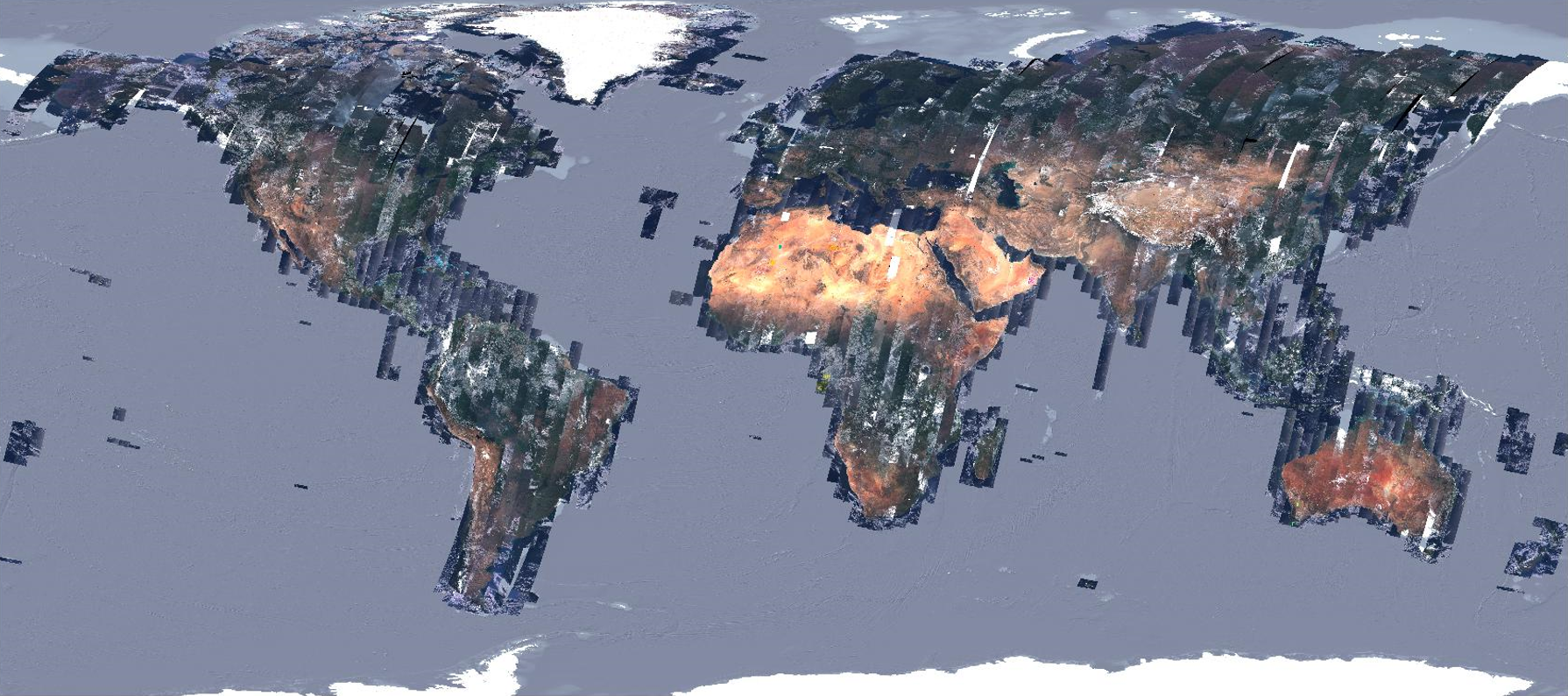
Figure 2: Overview of SENTINEL-2 GRI images
Products over Svalbard, isolated islands at high latitude and Antarctica are not covered by the GRI so are not refined. Moreover, several orbits covering Greenland and Northern Canada (Nunavut and Yukon territories) could not be completed. Please also note that orbit R109 is empty because it is almost totally located over sea.
For the last condition (similar geometry), it is necessary to resample the two segments in a common virtual geometry, because of SENTINEL-2 specificities: the images are split in 12 detectors and the pointing precision is at worst 2 kms.
This viewing model of the common virtual geometry is computed by:
- constructing an average regular datation model over the segment to refine,
- selecting the attitude and orbital data of the segment to refine
- and by computing regular viewing directions, as if it were a push-broom sensor, composed of one single detector, covering the whole SENTINEL-2 swath.
The two images are then resampled, using the resampling grids, an interpolation filter and the definition of interest area for each detector, as illustrated in Figure 3. Then the correlation is performed between two monolithic images composed of one single detector. This guarantees that the processing is homogeneous for all the detectors and allows detection of yaw angle. It has to be noticed that this common geometry is only used for the correlation process for finding GCP and is then discarded.
Figure 3: Resampling in a Monolithic Geometry
Tie points collection and filtering
A spatial correlation between a correlation window of reference image (vignette 1) and a research window image to refine (vignette 2) is performed for each pixel. Then, for each pixel of the vignette 2, a resemblance criterion is computed: it is the normalized covariance. The set of all criterion values make a grid of resemblance criteria. The maximum of correlation and a curvature are computed by fitting this grid of resemblance criteria to a quadratic function. The best candidate points coordinates correspond to the maximum of the quadratic function with high curvature. A threshold on the maximum correlation value and the curvature and a filter to eliminate wrong points are applied to obtain the homologous points.
This defines a set of tie points, as illustrated in Figure 4.
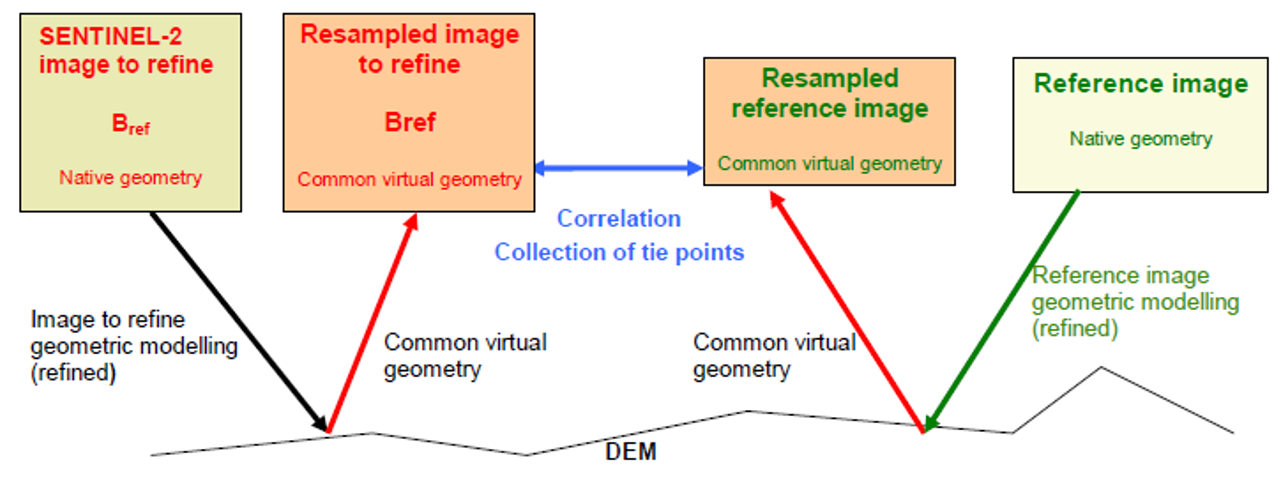
Figure 4: Tie points collection
This grid of measured differences between the two images is filtered in order to select tie points with a specific strategy: the image is divided into several areas (sub-scenes) and a given number of trusty tie points is required for each sub-scene. If the required number of points cannot be found in a given subscene, this area is densified using image matching with a lower step. If there are more tie points than the required number, a random selection is performed. The algorithm fails if it cannot get the requested number of points for a minimum number of sub-scenes.
From tie points to GCPs
Due to parallax between odd and event detectors, as shown in Figure 5, the tie-points need to be converted in native geometry.
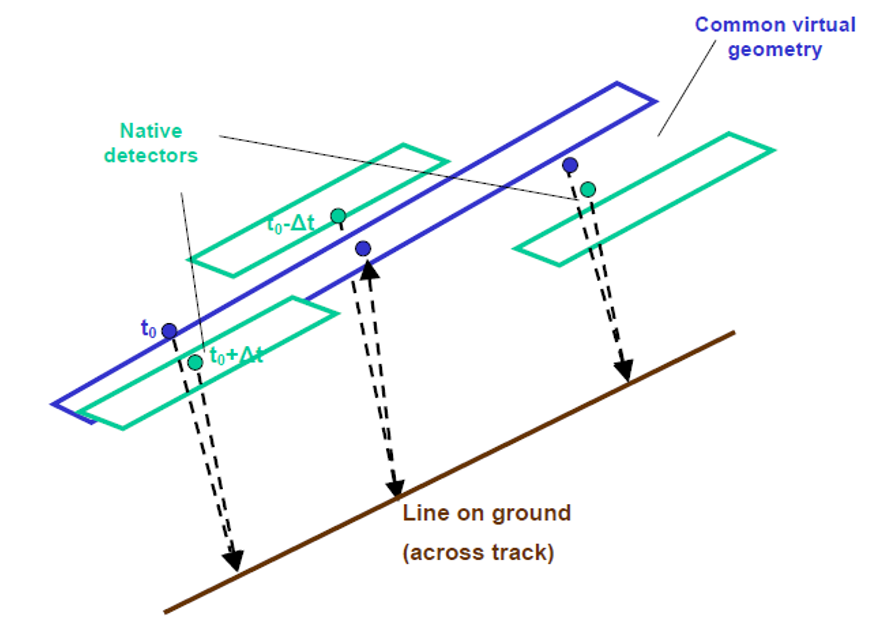
Figure 5: Line on ground seen at different dates by odd as even detectors
Then the tie-points coordinaFtes of the reference image are converted in geometric coordinates (latitude, longitude, altitude) using the DEM and the reference geometric model.
The following Figure 6 sums up the different steps, which take place for the conversion of tie points to ground control points.
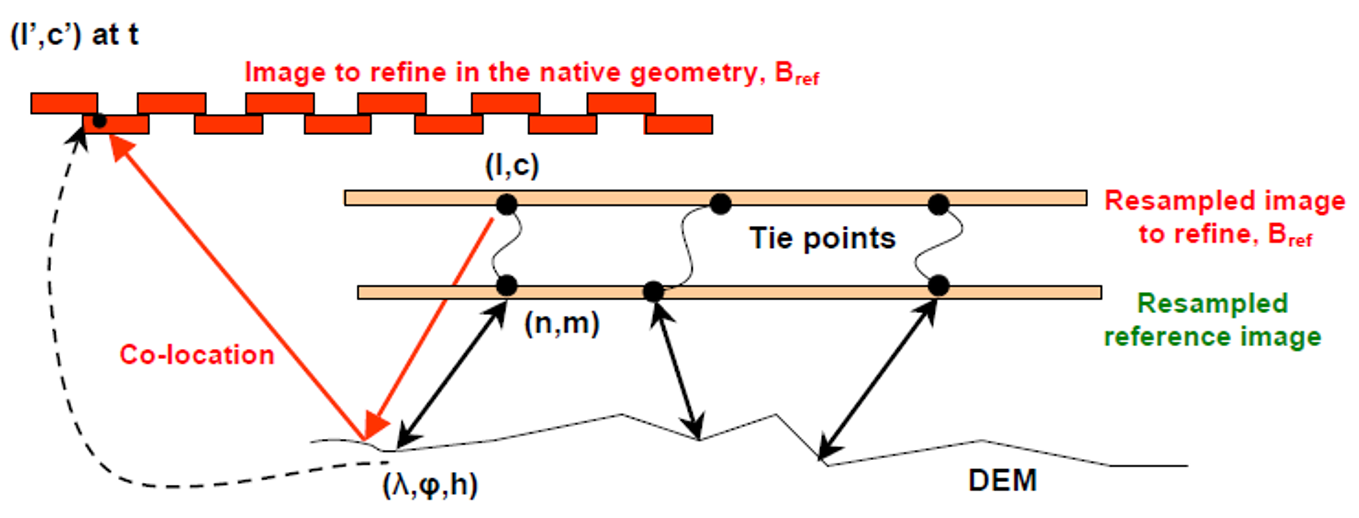
Figure 6: Tie points to GCPs conversion
Geometric refining
The geometric refining of the viewing model is done by spatio-triangulation using GCPs extracted at the previous step, with the parameters to refine and for each, the degree of the modelling polynomial function, chosen among:
- Spacecraft gravity centre position: X, Y, Z in WGS and type of correction: constant or polynomial function of time.
- Attitudes: roll, pitch and yaw, type of correction: constant or polynomial function of time.
- Spacecraft to focal plane transformation: rotation (3 angles), translation, homothetic transformation, type of correction: constant or polynomial function.
The default setting is given below and illustrated in Figure 7:
- Attitudes:
- roll, pitch, yaw in spacecraft frame
- correction modelled by a bias and a drift
- Spacecraft gravity centre position:
- X, Y, Z in WGS84
- correction modelled by a second-degree polynomial function
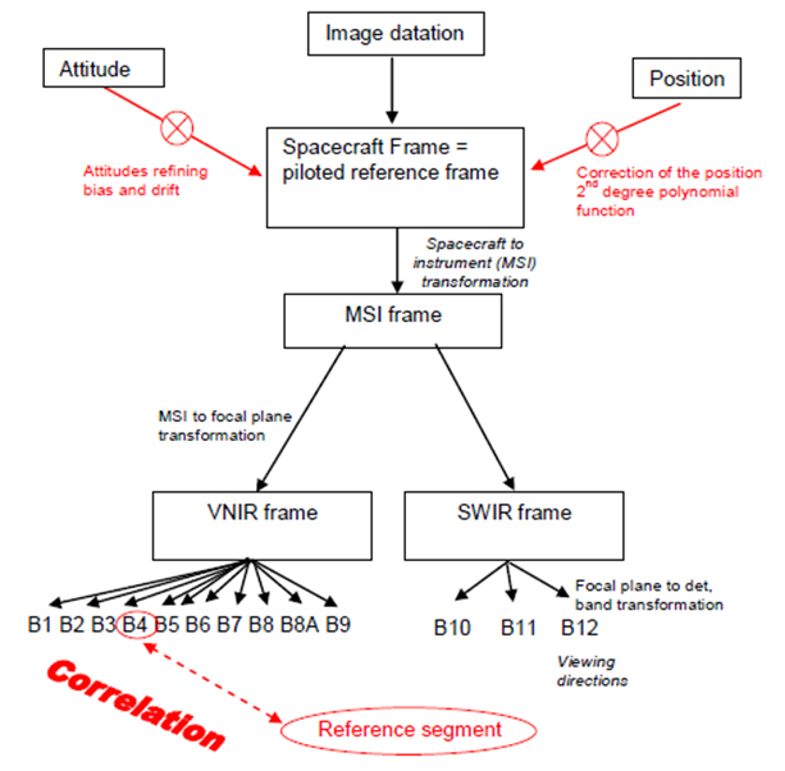
Figure 7: Viewing model and parameters to refine